[Linear Algebra] Part 02. Range, Null space, The determinant, Qaudratic Forms and Definitiveness, Eigenvalues and Eigenvectors

 개념을 정리하기 위해 2019년도 Stanford University에서 진행한 CS229: Machine Learning - The Summer Edition 강의와 강의 노트를 참고하였고, 본 코스에 들어가기 전에 진행되는 Pre-requisties review 파트를 통해 공부하고 정리했습니다.

 

지난 글에서는 Lecture 1에서 다룬 선형대수의 기본적인 개념 및 notation, matrix multiplication, operation and properties (~orthogonal matrices) 부분에 대해 살펴보았습니다. 이어서 이번 글에서는 Lecture 1 후반부, Lecture 2 중반부까지 다루는 Operation and Properties의 뒷부분(Range and nullspace of a matrix, The determinant, Quadratic forms and definitivess, Eigenvalues and eigenvectors)에 대해 다뤄볼 것입니다.

 

그럼 시작하겠습니다.

 

3. Operation and Properties

- Range and Nullspace of matrix

$ \quad $ range와 nullspace에 대해 알아보기 전에 span 의 개념을 먼저 알아야 합니다. 벡터 집합의 span이라는 것은 구성하고 있는 벡터들의 linear combination으로 표현할 수 있는 모든 벡터들의 집합을 의미합니다. 만약, $x_1$ 부터 $x_n$까지의 모든 벡터들이 서로 linearly independent 하다면, 이 벡터들이 span 한 공간은 $\mathbb{R}^n$을 이룰 것입니다. 즉, 어떠한 벡터 $v \in \mathbb{R}^n$라도 $x_1$ 부터 $x_n$까지의 벡터들의 linear combination으로 표현할 수 있다는 것을 의미합니다.

$span(\left \{ x_1, \cdots, x_n \right \})=\left \{ v: v=\sum_{i=1}^{n}\alpha_ix_i, \quad \alpha_i \in \mathbb{R}  \right \}$

 

$ \quad $ projection(투영)에 대해서도 간단히 살펴보겠습니다. projection이란, 어떠한 벡터 $y \in \mathbb{R}^m$를 $\left \{ x_1, \cdots, x_n \right \}$이 span 한 공간 위에 수직으로 투영시키는 작업이라고 할 수 있겠습니다. 따라서 투영시킨 벡터는 span 된 공간 안에 포함되게 될 것입니다. 이때, 투영된 벡터 $v \in \left \{ x_1, \cdots, x_n \right \}$ 는 Euclidean norm에 의해 측정했을 때, 벡터 y와 가장 가까운 벡터라고 할 수 있습니다.

$Proj(y; \left \{ x_1, \cdots, x_n \right \})={argmin}_{v \in span \left \{ x_1, \cdots, x_n \right \}} {\left \| y-v \right \|}_2$

$ \quad $ 예를 들어, 2차원 공간에서 투영 벡터를 구하는 식은 다음과 같습니다. 벡터 v를 구한 최종 식을 기억하고 있으면 될 것 같습니다.

projection vector를 구하는 식을 유도하는 과정

 

$ \quad $ 여기서 Range 에 대해 정의해보겠습니다. 행렬 A에 대해서, A의 range는 행렬 A의 column들을 span한 공간입니다. 즉, A의 range는 행렬 A의 column space라고도 할 수 있습니다. $Ax=b$ 라는 행렬과 벡터 간의 연산에서 행렬 A를 function이라고 생각하면, 벡터 x를 input값으로 넣었을 때, b라는 벡터를 output으로 얻을 수 있을 것입니다. 이때, range는 output으로 나올 수 있는 모든 벡터 b의 집합인 치역과 같은 의미라고 할 수 있습니다.

The range of A

$ \quad $ Range의 표기는 다음과 같습니다. $ \quad (A \in \mathbb{R}^{m \times n})$

$R(A)=\left \{ Ax|x\in \mathbb{R}^n  \right \}$

$ \quad $ 앞서 소개했던 벡터 간의 projection과 유사하게 여러 벡터들이 모여 이루어진 행렬, 즉 multiple vector들이 span 한 공간 위의 projection vector을 구하는 식 또한 비슷하게 구할 수 있습니다.

$Proj(y; A)={argmin}_{v \in R(A)} {\left \| v-y \right \|}_2=A{(A^TA)}^{-1}A^Ty$

 

$ \quad $ 다음은 nullspace(영 공간)입니다. Nullspace는 행렬 A와 곱해져서 0이 되는 모든 벡터 x들의 집합을 의미합니다. $A \in \mathbb{R}^{m \times n}$에 대해, $R(A)$의 사이즈는 m이고, $N(A)$의 사이즈는 n입니다. 이때 $R(A^T)$의 사이즈는 n, 즉 A의 row space의 사이즈는 n이므로 n차원의 벡터들을 아래와 같이 표현하여 row space의 벡터와 nullspace의 벡터의 합으로 표현할 수 있습니다.

$\left \{ w:w=u+v, \quad u \in R(A^T), v \in N(A) \right \}= \mathbb{R}^n$

$ \quad A^T$의 range와 nullspace는 n차원 공간을 이루는 disjoint subset(서로소 관계)입니다. 이와 같은 것들을 orthogonal complements라고 부릅니다.

 

- The Determinant (행렬식)

$ \quad $ 행렬식 determinant는 $n \times n$의 square matrix를 1차원의 스칼라 값으로 바꿔주는 함수라고 할 수 있습니다. ($ \mathbb{R}^{n \times n} \rightarrow \mathbb{R}$) Determinant는 $|A|$ 또는 $det A$로 표기하고 있습니다.

$ \quad $ Determinant에 대해 알아보기 위해, 기하학적인 해석을 통해 접근해보도록 하겠습니다. 우선 집합 S에 대해 정의하는데, 이 집합 S는 $ \left \{ x_1, \cdots, x_n \right \} $가 각 벡터$x_i$에 $0 \le \ \alpha_i \le 1$ 라는 계수가 곱해져서 선형 조합을 이룬 제한된 span 공간을 의미합니다.

$S=\left \{ v \in \mathbb{R}^n: v=\sum_{i=1}^{n}\alpha_ia_i \quad where \; 0 \le \alpha_i \le 1, i=1, \cdots, n \right \}$

$ \quad $ 이렇게 만들어지는 집합 S는 n-dimensional parallelotope(n차원 평행체)를 이루게 되는데, 이 도형의 부피가 바로 행렬 A의 determinant 절댓값을 의미합니다.

The volume of the set S is the absolute value of det A

$ \quad $ 다음은 determinant의 대수적인 속성들입니다. 다음 속성들에 대해서도 기하적인 의미를 생각한다면 쉽게 납득할 수 있을 것입니다.

$ \quad $ 우선 Identitiy matrix의 부피는 1이 나올 것이므로, $det \; I$는 당연히 1이 될 것입니다. 또한, matrix의 한 행에만 t라는 스칼라 값을 곱해주게 되면, 당연히 점들의 집합인 S가 한쪽으로만 scaling 될 것이므로, $det \; A$에 t배만큼 스칼라 곱한 값이 나오게 될 것입니다. 마지막으로, 행렬 A의 어떠한 두 행을 바꿔준 행렬의 determinant 값은 원래 determinant 값에 부호가 반대로 된 결과가 나오게 되는데, 이는 벡터들의 오른손 법칙을 생각한다면 쉽게 이해할 수 있을 것입니다.

$ \quad $ 위의 속성들로 다른 여러 가지 특징들을 도출해낼 수 있는데, 다음과 같습니다. $ \quad (A, B \in \mathbb{R}^{m \times n})$

• $|A| = |A^T|$
• $|AB| = |A||B|$
• A가 singular(non-inveretible)하다면, $ \quad |A|=0$
• A가 non-singular(inveretible)하다면, $ \quad |A^{-1}| = 1/|A|$

$ \quad $ 일반적으로 determinant를 구하는 식은 아래와 같습니다. (이때, $|A_{\backslash i, \backslash j}| $는 A에서 i번째 행과 j번째 열을 뺀 행렬의 determinant값을 의미합니다.)

$ \quad $ 또한, $A \in \mathbb{R}^{n \times n}$가 non-singular 할 때, A의 inverse(역행렬)도 구할 수 있고, 그 식은 다음과 같습니다.

 

- Quadratic Forms (이차형식) and Definitiveness

$ \quad $ 행렬 $A \in \mathbb{R}^{m \times n}$ 와 벡터 $x \in \mathbb{R}^n$ 가 주어졌을 때, $x^TAx$ 는 스칼라 값을 가지며, 이 식을 quadratic form 이라고 부르고 있습니다. 

$ \quad $ 일반적으로 행렬 A를 symmetric matrix라고 설정하는데, 이에 대해 살펴보자면 다음과 같습니다.

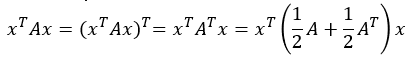
$ \quad $ 우선 $x^TAx$ 는 스칼라 값을 나타내기 때문에 스칼라 값에 transpose를 취해주어도 변화가 없다는 사실을 이용해 $x^TAx$ 에 transpose를 취해줍니다. transpose의 속성 때문에 $x^TA^Tx$ 가 되게 되고, 이를 symmetric-anti symmetric matrix 판별? 하는 식을 이용하면 마지막 결과를 얻을 수 있게 됩니다. 이를 통해 quadratic form에 등장하는 행렬은 symmetric 하다고 할 수 있습니다.

 

$ \quad $ 이어서, definitiveness에 대해 살펴보겠습니다. Square 하고 Symmetric 한 행렬 $A \in \mathbb{R}^{n \times n}$에 대한 quadratic form의 결과에 주목합니다.

• Non-zero 벡터인 모든 벡터 $x$에 대해서 $x^TAx > 0$ 이라면, $ \quad A$는 positive definite (PD). $\quad (A \succ 0, \quad {\mathbb{S}^n}_{++} ) $ 
• 모든 벡터 $x$에 대해서 $x^TAx \ge 0$ 이라면, $ \quad A$는 positive semidefinite (PSD). $\quad (A \succeq 0, \quad {\mathbb{S}^n}_{+} ) $
• Non-zero 벡터인 모든 벡터 $x$에 대해서 $x^TAx < 0$ 이라면, $ \quad A$는 negative definite (ND). $\quad (A \prec 0) $
• 모든 벡터 $x$에 대해서 $x^TAx \le 0$ 이라면, $ \quad A$는 negative semidefinite (NSD). $\quad (A \preceq 0) $
• ${x_1}^TAx_1 > 0, \; {x_2}^TAx_2 > 0$ 을 만족하는 벡터 $x_1, x_2 \in \mathbb{R}^n$가 존재한다면, $ \quad A$는 indefinite.

$ \quad $ 또한, positive definite와 negative definite인 행렬은 항상 full rank인 성질을 가지고 있습니다. 만약, 행렬 A가 full rank가 아니고 어느 한 행이 다른 행들의 linear combination으로 이루어져 있다고 가정해보겠습니다. $Ax$ 연산이 이루어질 때, linear combination으로 이루어진 dependent 한 행에 붙는 계수가 -1이면 $Ax$ 의 결과는 0이 될 것이고, $x^TAx$ 의 결과 또한 0이 되어 semidefinite 하다는 결과가 나오게 될 것입니다. 따라서, positive or negative definite인 행렬은 항상 full rank 하다는 결론이 나오게 됩니다.

$ \quad $ 그리고, symmetric하지 않고 square하지 않은 행렬 $A \in \mathbb{R}^{m \times n}$이 주어졌을 때, 이를 symmetric & square 행렬로 바꿔주는 방법이라고 할 수 있는 Gram matrix $\; G=A^TA \; $는 항상 positive semidefinite라는 특징이 있습니다. 이때, $m>n$이고 $A$가 full rank 라면, $G$는 positive definite입니다.

 

- Eigenvalues and Eigenvectors (고윳값과 고유 벡터)

$ \quad $ Square matrix인 $A \in \mathbb{R}^{n \times n}$가 주어질 때, $\; Ax=\lambda x$ 의 방정식을 이루는 $\lambda$를 eigenvalue 라 하고, 그 eigenvalue에 대응하는 벡터 x를 eigenvector 라고 합니다. 이를 다시 말하자면, $Ax$의 결과로 나온 새로운 벡터가 벡터 x의 방향과 같고 크기만 다르게 scaling 된 경우를 말합니다.

$Ax=\lambda x \quad (x \ne 0)$

Ax가 기존 벡터 x의 방향대로 scaling만

$ \quad $ 위의 식을 다시 쓰게 되면, 다음과 같이 정리할 수 있습니다.

$(\lambda I - A)x=0 \quad (x \ne 0)$

$ \quad $ 행렬 $A$의 $\lambda$가 존재하기 위해서는 $x$가 0이 아닌 해가 존재해야 하므로, $(\lambda I - A)$는 singular 해야 합니다. 따라서, $det(\lambda I - A)$ 값은 0이 되어야 하고, 이 행렬식은 eigenvalue $\lambda$에 대한 n차 다항식이며 $A$의 특성 방정식 또는 특성 다항식이라고 합니다.

$det(\lambda I - A)=0$

$ \quad A \in \mathbb{R}^{n \times n}$이고, eigenvalues를 $\lambda_i, \cdots , \lambda_n$이라고 할 때, eigenvalue와 eigenvector의 속성을 정리해보겠습니다.

• $trA=\sum_{i=1}^{n}\lambda_i$
• $|A|=\prod_{i=1}^{n}\lambda_i$
• $A$의 rank는 $A$의 0이 아닌 eigenvalue의 수와 같습니다.
• A가 non-singular 행렬(가역 행렬)이면, $A^{-1}$의 eigenvalue는 $1/\lambda$
• diagonal matrix $D$의 eigenvalue는 대각 성분들입니다. $(d_1, d_2, \cdots, d_n)$

 

- Eigenvalues and Eigenvectors of Symmetric matrices

$ \quad A$가 실수로 이루어진 symmetric matrix라고 두고 진행해보겠습니다.

1. 모든 eigenvalue도 모두 실수입니다. ($\lambda_1, \cdots, \lambda_n$)
2. eigenvector들을 $u_1, \cdots, u_n$이라 하고 이 eigenvector들로 이루어진 orthonormal 한 matrix를 $U$라고 합니다.

$U = \begin{bmatrix}
| & | &  & | \\ 
u_1 & u_2 & \cdots & u_n \\ 
| & | &  & |
\end{bmatrix}$

 

$ \quad $ 이때, eigenvalue값들을 대각 성분으로 구성하고 있는 대각 행렬을 $\Lambda$라고 하겠습니다. A와 U의 matrix product를 표현하면 다음과 같이 column들로 표현할 수 있습니다. 이때, $Ax=\lambda x$ 식을 이용해 $Au_i=\lambda u_i$로 나타낼 수 있고, 이를 $U$와 $\Lambda$의 곱으로 나타낼 수 있게 됩니다.

$AU = \begin{bmatrix}
| & | &  & | \\ 
Au_1 & Au_2 & \cdots & Au_n \\ 
| & | &  & |
\end{bmatrix}=\begin{bmatrix}
| & | &  & | \\ 
\lambda_1u_1 & \lambda_2u_2 & \cdots & \lambda_nu_n \\ 
| & | &  & |
\end{bmatrix}=U\Lambda$

$ \quad $ 여기서, orhonormal matrix의 특징인 $\; UU^T=I$를 통해 $A$를 다음과 같이 나타낼 수 있고, 이를 $A$의 diagonalization (대각화)라고 합니다.

$A=AUU^T=U \Lambda U^T$

$ \quad $ 또한, 어떠한 벡터 $x \in \mathbb{R}^n$ 라도 eigenvector들의 linear combination 으로서 표현할 수 있고, 이를 통해 벡터 x를 다르게 표현할 수 있습니다.

$x = \hat{x}_1u_1 + \cdots + \hat{x}_nu_n = U \hat{x}$ 

$x = U \hat{x} \quad \Leftrightarrow \quad \hat{x} = U^Tx$

$ \quad $ 마지막으로, matrix-vector 연산에 대해서도 diagonalizing(대각화)를 수행할 수 있습니다. 벡터 $z=Ax \;$라 두고 matrix-vector 곱에 대해 살펴 보겠습니다.

$\hat{z} = U^Tz = U^TAx = U^TU \Lambda U^Tx = \Lambda \hat{x} = \begin{bmatrix}
\lambda_1 \hat{x}_1\\ 
\lambda_2 \hat{x}_2\\ 
\vdots \\ 
\lambda_n \hat{x}_n
\end{bmatrix}$

$ \quad $ 이를 통해, matrix-vector 연산인 $Ax \;$에 대해서도 새로운 basis 관점에서 diagonal matirx 와의 곱으로서 표현 가능하게 됩니다.

 

 

 

* 이해가 되지 않거나 수정해야 할 부분이 있다면, 언제든지 댓글 부탁드립니다. 감사합니다.